포스트

동적 계획법(DP, Dynamic Programming)

게시
By 신건우 11 분읽는 시간

Richard Bellman이 1950년대에 사용한 단어

기본적인 아이디어

하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용

동적 계획법을 가장 잘 설명하는 단어는 ‘기억하며 풀기’

특정한 알고리즘이 아닌 하나의 문제해결 방법론으로 바라보는 것이 적절하다

왜 DP를 사용?

일반적인 재귀 방식은 DP와 매우 유사하다.

하지만 큰 차이점은 일반적인 재귀를 단순 사용 시 동일한 작은 문제들이 여러 번 반복 되어 비효율적인 계산을 할 수 있다는 것이다.

예시 : 피보나치 수열

출처 : https://hongjw1938.tistory.com/47

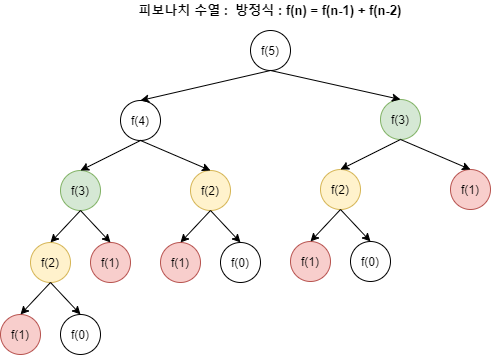
​ 피보나치 수열의 경우 큰 문제인 f(5)의 값을 계산해내기 위해 동일한 계산인 f(0)을 3번, f(1)을 5번 계산해야 한다.

​ 그러나 한 번 구한 작은 문제의 결과 값을 저장해두고 재사용 한다면, 매우 효율적으로 문제를 해결할 수 있게 된다.

\[O(n^2) \to O(f(n))\]

DP의 적용 조건

  1. Overlapping Subproblems(겹치는 부분 문제)

    DP는 기본적으로 문제를 나누고 그 문제의 결과 값을 재활용해서 전체 답을 구한다. 동일한 작은 문제들이 반복하여 나타나는 경우에 사용이 가능하다.

    피보나치의 경우 f(0), f(1), 등등이 반복되는 동일한 부분 문제다.

  2. Optimal Substructure(최적 부분 구조)

    부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우를 의미한다. 그래서 특정 문제의 정답은 문제의 크기에 상관없이 항상 동일하다.(동일한 해결 방식으로 최적 해를 구할 수 있다.)

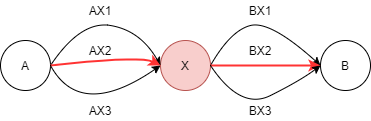
    A와 X 사이의 최단 거리가 AX2

    X와 B 사이의 최단 거리가 BX2일때

    A-X-B 사이의 최단 거리(최적해)는 두 부분 문제의 최단거리(최적해)의 합으로 표현 가능, 즉 AX2+BX2

    이 경우 최적 부분 구조를 가진다고 말할 수 있다.

DP 사용하기

  1. DP로 풀 수 있는 문제인지 확인한다. (DP 적용 조건 2가지 check)

    현재 직면한 문제가 중복된 작은 문제들로 이루어진 하나의 함수로 표현 가능한가?

    예시

    • 데이터 내 최대화 / 최소화 계산
    • 특정 조건 내 데이터 count
    • 확률 계산

  2. 문제의 변수 파악

    DP는 현재 변수(variable)에 따라 그 결과 값을 찾고 그것을 전달,저장하여 재사용하는 과정을 거친다.

    즉, 문제 내 변수(variable)의 개수를 알아내야 한다는 것이다.

    더 자세하게는 해 공간(state space)에서의 현재 위치(state)를 결정하는 변수의 종류와 개수에 대해 알아야 한다. state는 문제의 해결 과정에서 어디에 위치하고 있는지를 나타내며, 이 위치는 문제의 변수들에 의해 결정된다.

    DP에서는 state를 사용하여 문제를 여러 하위 문제로 분해한다.

    예시

    • 피보나치 수열

      n번째 숫자를 구하는 것이므로 n이 변수가 된다.

    • 문자열 간의 차이

      문자열의 길이, Edit 거리

    • Knapsack 문제

      아이템의 index, 아이템의 무게

  3. 변수 간 관계식 만들기

    변수들에 의해 결과 값이 달라지나, 동일한 변수값인 경우 결과는 동일하다. 또한 결과값을 그대로 이용할 것이므로, 변수값과 결과값 사이의 관계식을 만들어낼 수 있어야 한다.

    그런 관계식을 점화식이라고 부르며, 점화식의 반복/재귀를 통해 문제가 해결되도록 코드를 작성한다.

    예시

    • 피보나치 수열에서는 $f(n)=f(n-1)+f(n-2)$이다.

  4. 메모하기 (memoization or tabulation)

    변수의 값에 따른 결과를 저장하는 부분이다.

    메모한다고 하여 Memoization이라고 부른다.

    변수 값에 따른 결과를 저장할 배열(딕셔너리)을 미리 만들고 새로운 결과가 나올 때마다 배열에 저장하고 저장된 값을 재사용하는 방식으로 문제를 해결해 나간다.

    결과를 저장할 때는 배열이나 딕셔너리를 사용할 수 있는데, 각각의 장단점에 대해서 생각해보고 적절하게 사용하면 된다.

  5. 기저 상태 파악하기

    가장 작은 문제의 상태를 알아야 한다. 보통 몇 가지 예시를 손으로 테스트하여 구성하는 경우가 많다.

    해당 기저 문제에 대해 파악 후 미리 배열에 저장해둔다.

    예시

    • 피보나치 수열의 경우, 가장 작은 문제는 다음과 같다.

      $f(0) = 0$

      $f(1) = 1$

      이후 두 숫자를 더해가며 값을 구하지만 가장 작은 문제는 이 2가지다.

  6. 구현하기

    DP는 2가지 방식으로 구현할 수 있다.

    1. Bottom-Up(Tabulation) - 반복문 사용

      아래부터 계산을 수행하고 누적시켜 전체 문제를 해결하는 방식

      메모를 위해서 dp라는 1차원 배열을 만들었다.

      dp[0]이 기저 상태이고, dp[n]을 목표 상태라고 한다면, Bottom-up은 dp[0]부터 시작하여 반복문을 통해 점화식으로 결과를 내어 dp[n]까지 값을 전이시켜 재활용하는 방식이다.

      • Tabulation?

        Memoization과 근본적으로 다르지 않으나 Bottom-up일 때는 Tabulation이라고 부른다.

        반복을 통해 dp[0]부터 하나 하나씩 채우는 과정을 “table-filling” 하며, 이 Table에 저장된 값에 직접 접근하여 재활용하므로 Tabulation이라는 명칭이 붙었다고 한다.

    2. Top-Down(Memoization) - 재귀 사용

      위에서 부터 호출을 시작하여 기저 상태까지 내려간 다음 결과 값을 재귀를 통해 전이시켜 재활용하는 방식

    구현 예시

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

     import time
    
 # DP를 사용 시 작은 문제의 결과값을 저장하는 배열
 # Top-down, Bottom-up 별개로 생성하였음(큰 의미는 없음)
 topDown_memo = []
 bottomup_table = []
    
 # 단순 재귀를 통해 Fibonacci를 구하는 경우
 # 동일한 계산을 반복하여 비효율적으로 처리가 수행됨
 def naiveRecursion(n):
     if n <= 1:
         return n
     return naiveRecursion(n-1) + naiveRecursion(n-2)
    
 # DP Top-Down을 사용해 Fibonacci를 구하는 경우
 def topDown(n):
     # 기저 상태 도달 시, 0, 1로 초기화
     if n < 2: 
         return topDown_memo[n]
        
     # 메모에 계산된 값이 있으면 바로 반환!
     if topDown_memo[n] > 0: 
         return topDown_memo[n]
        
     # 재귀를 사용하고 있음!
     topDown_memo[n] = topDown(n-1) + topDown(n-2)
        
     return topDown_memo[n]
    
 # DP Bottom-Up을 사용해 Fibonacci를 구하는 경우
 def bottomUp(n):
     # 기저 상태의 경우 사전에 미리 저장
     bottomup_table[0] = 0
     bottomup_table[1] = 1
        
     # 반복문을 사용하고 있음!
     for i in range(2, n+1):
         # Table을 채워나감!
         bottomup_table[i] = bottomup_table[i-1] + bottomup_table[i-2]
     return bottomup_table[n]
    
 def main():
     n = 40
     global topDown_memo, bottomup_table
     topDown_memo = [0]*(n+1)
     topDown_memo[0] = 0
     topDown_memo[1] = 1
     bottomup_table = [0]*(n+1)
        
     startTime = time.time()
     print(naiveRecursion(n))
     endTime = time.time()
     print(f"일반 재귀 소요 시간 : {endTime - startTime}")
        
     print()
        
     startTime = time.time()
     print(topDown(n))
     endTime = time.time()
     print(f"Top-Down DP 소요 시간 : {endTime - startTime}")
        
     print()
        
     startTime = time.time()
     print(bottomUp(n))
     endTime = time.time()
     print(f"Bottom-Up DP 소요 시간 : {endTime - startTime}")
    
 if __name__ == "__main__":
     main()
    
 # 결과 동일

참고 자료

알고리즘 - Dynamic Programming(동적 계획법)

GPT-4

Algorithm, Structure
Algorithm DP
이 기사는 저작권자의 CC BY 4.0 라이센스를 따릅니다.